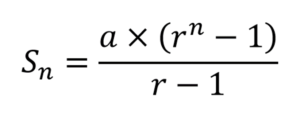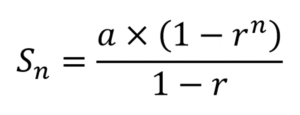BARISAN BILANGAN GENAP
| Barisan | 2, 4, 6, 8, 10, ……. |
| Deret | 2 + 4 + 6 + 8 + 10 + ……. |
| Suku ke-n | Un = 2n |
| Jumlah n suku pertama | Sn = n2 + n |
BARISAN BILANGAN GANJIL
| Barisan | 1, 3, 5, 7, 9, ……. |
| Deret | 1 + 3 + 5 + 7 + 9 + ……. |
| Suku ke-n | Un = 2n – 1 |
| Jumlah n suku pertama | Sn = n2 |
BARISAN BILANGAN PERSEGI (KUADRAT)
| Barisan | 1, 4, 9, 16, 25, ……. |
| Deret | 1 + 4 + 9 + 16 + 25 + ……. |
| Suku ke-n | Un = n2 |
| Jumlah n suku pertama | Sn = (1/6) n (n + 1) (2n + 1) |
BARISAN BILANGAN KUBUS (KUBIK)
| Barisan | 1, 8, 27, 64, 125, ……. |
| Deret | 1 + 8 + 27 + 64 + 125 + ……. |
| Suku ke-n | Un = n3 |
| Jumlah n suku pertama | Sn = (1/4) n2 (n + 1)2 |
BARISAN BILANGAN SEGITIGA
| Barisan | 1, 3, 6, 10, 15, ……. |
| Deret | 1 + 3 + 6 + 10 + 15 + ……. |
| Suku ke-n | Un = (1/2) n (n + 1) |
| Jumlah n suku pertama | Sn = (1/6) n (n + 1) (n + 2) |
BARISAN BILANGAN PERSEGI PANJANG
| Barisan | 2, 6, 12, 20, 30, ……. |
| Deret | 2 + 6 + 12 + 20 + 30 + ……. |
| Suku ke-n | Un = n (n + 1) |
| Jumlah n suku pertama | Sn = (1/3) n (n + 1) (n + 2) |
BARISAN BILANGAN BALOK
| Barisan | 6, 24, 60, 120, 210, ……. |
| Deret | 6 + 24 + 60 + 120 + 210 + ……. |
| Suku ke-n | Un = n (n + 1) (n + 2) |
| Jumlah n suku pertama | Sn = (1/4) n (n + 1) (n + 2) (n + 3) |
BARISAN BILANGAN FIBONACCI
| Barisan | 1, 1, 2, 3, 5, 8, 13, 21, ……. |
| Deret | 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + ……. |
| Suku ke-n | Un = U(n-1) + U(n-2) *hitung manual |
| Jumlah n suku pertama | Sn = *hitung manual |
BARISAN ARITMATIKA
| Catatan: | a = suku pertama |
| b = beda (selisih antarsuku yang selalu bernilai sama) | |
| n = banyaknya suku | |
| ! (dibaca: faktorial) = perkalian hitung mundur dari suati angka | |
| misal:
3! (dibaca: 3 faktorial) = 3 × 2 × 1 = 6 |
| Barisan | 1, 2, 3, 4, 5, ……. *dalam contoh ini, a = 1 dan b = +1 |
| Deret | 1 + 2 + 3 + 4 + 5 + ……. |
| Suku ke-n | Un = a + (n – 1) b |
| Jumlah n suku pertama | Sn = (1/2) n (a + Un)
atau Sn = (1/2) n (2a + (n – 1) b) |
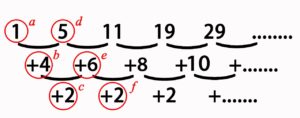
| BARISAN ARITMATIKA BERTINGKAT (2 tingkat)
Contoh:
|
|
| Suku ke-n | 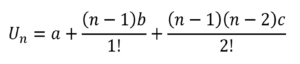 |
| Jumlah n suku pertama | 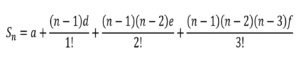 |
BARISAN GEOMETRI
| Catatan: | a = suku pertama |
| r = rasio antarsuku | |
| n = banyaknya suku |
| Barisan | 1, 2, 4, 8, 16, 32, ……. *dalam contoh ini, a = 1 dan r = ×2 |
| Deret | 1 + 2 + 4 + 8 + 16 + 32 + ……. |
| Suku ke-n | Un = a × r(n – 1) |
| Jumlah n suku pertama | untuk r ≥ 1
untuk r < 1
|